Vertical Line Test: How to Apply? Why It works? Examples, Applications, Misconceptions & FAQs

The vertical line test is a straightforward graphical method used to determine whether a given curve represents a function.

In mathematics, a function is defined as a relation where each input (\( x \)-value) corresponds to exactly one output (\( y \)-value).

The vertical line test helps verify this by analyzing the graph of the relation.

How to Apply the Vertical Line Test

1. Draw Vertical Lines: Imagine or draw vertical lines (parallel to the \( y \)-axis) across the entire graph of the relation.
2. Observe Intersections: For each vertical line, observe the number of intersection points with the graph.
3. Interpret Results:

• Function: If every vertical line intersects the graph at no more than one point, the graph represents a function. This indicates that each \( x \)-value has a unique \( y \)-value.
• Not a Function: If any vertical line intersects the graph at more than one point, the graph does not represent a function. This suggests that at least one \( x \)-value corresponds to multiple \( y \)-values, violating the definition of a function.

Illustrative Examples

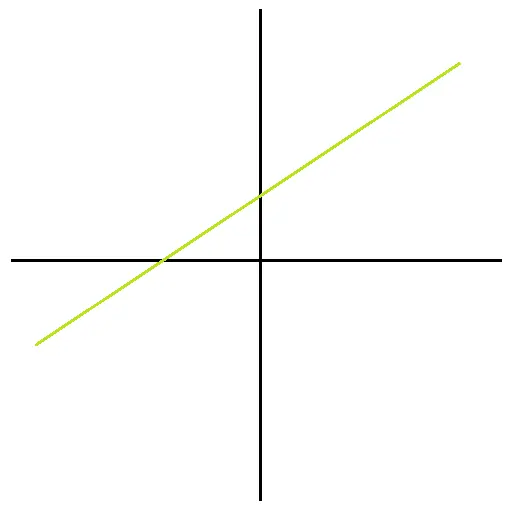
• Example 1: Linear Function Consider the graph of the equation (\( y = x \)), which is a straight line passing through the origin at a 45-degree angle. When applying the vertical line test, any vertical line will intersect this graph at exactly one point, confirming that it is a function.
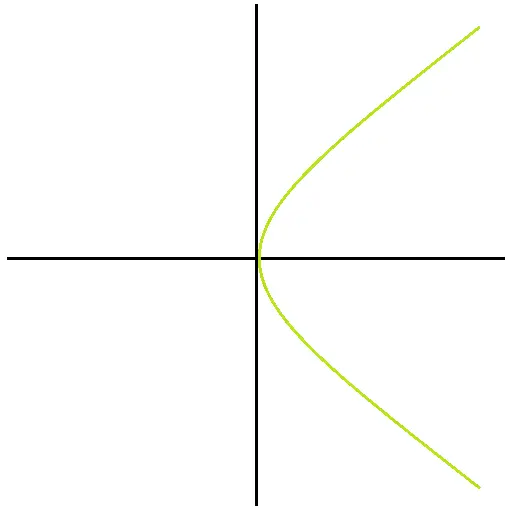
• Example 2: Parabola Opening to the Right Now, consider the graph of the equation (\( x = y^2 \)), which is a parabola opening to the right. Applying the vertical line test, some vertical lines will intersect the graph at two points, indicating that it is not a function.

Why the Vertical Line Test Works

The vertical line test is effective because it directly assesses the fundamental definition of a function: each input must map to a single output.

If a vertical line intersects the graph more than once, it means a single \( x \)-value is associated with multiple \( y \)-values, thereby disqualifying the relation from being a function.

Applications in Mathematics Education

Understanding and applying the vertical line test is crucial for students as it:

• Enhances Graphical Analysis Skills: Enables students to visually interpret and analyze graphs to determine functional relationships.
• Supports Function Identification: Assists in distinguishing between functions and non-functions, which is fundamental in higher-level mathematics.
• Facilitates Understanding of Function Properties: Aids in comprehending the behavior and properties of different types of functions.

Common Misconceptions:

• Misinterpretation of Intersections: Some students may mistakenly believe that intersecting at multiple points does not violate function rules. It’s essential to emphasize that multiple intersections by a vertical line indicate multiple outputs for a single input, which is not permissible in functions.
• Applicability to All Graphs: The vertical line test applies to all graphs, including those of discrete and continuous relations.

Finalizing

The vertical line test is a valuable tool in mathematics for identifying whether a graph represents a function.

By ensuring that each input has a unique output, it reinforces the foundational concept of functions and aids in the accurate analysis of mathematical relations.

Frequently Asked Questions (FAQs)